
Exploring Pedal Triangles
by
Susan Sexton
What is a pedal triangle?
Take an arbitrary point
outside of a given triangle.
Construct the perpendicular lines to each of the lines containing each
side of the given triangle from the arbitrary point. Connecting the three intersections of the perpendicular
lines to the lines containing each of the three sides will form a
triangle. This triangle is the
pedal triangle.
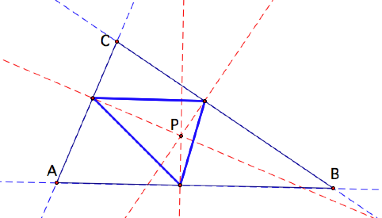
Below is a figure
illustrating a pedal triangle formed from point P in the plane with given
triangle ABC.
Here is a GSP sketch to move
P around and see what happens to the pedal triangle.
While P is noted to be an
arbitrary point, it would be interesting to see what happens when P is located
at certain points in regards to the triangle.
What happens when P is one of the centers of the
triangle?
Incenter:
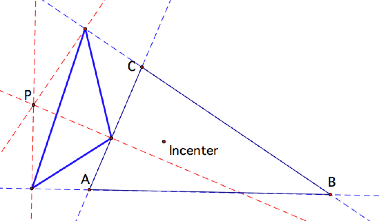
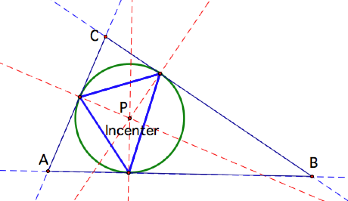
P is the circumcenter of the Pedal Triangle!
Orthocenter:
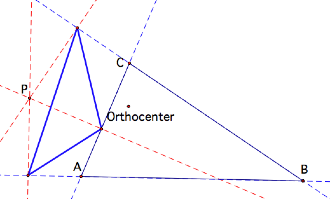
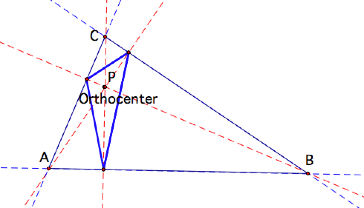
The pedal triangle becomes the orthic triangle!
What if the Orthocenter is
outside the triangle?
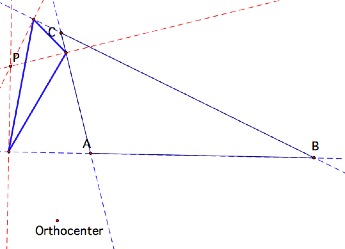
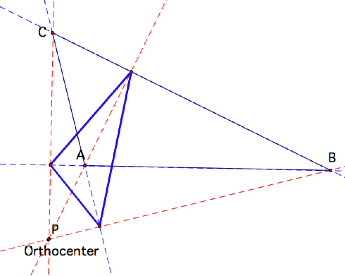
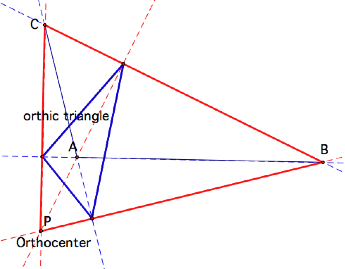
The pedal triangle becomes the orthic triangle to the
triangle whose vertices are C, B and the orthocenter of triangle ABC.
Circumcenter
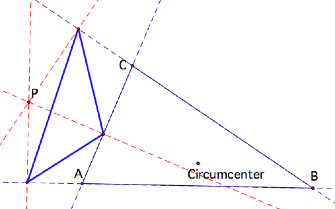
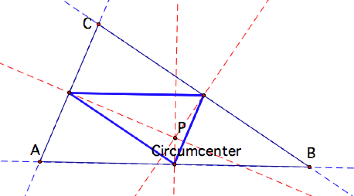
The pedal triangle is the same as the medial triangle!
Why is this?
The pedal triangle is created by the perpendicular bisectors of each side thus making its vertices the midpoints
of each side.
What if the Circumcenter is
outside the triangle?
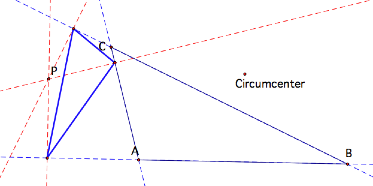
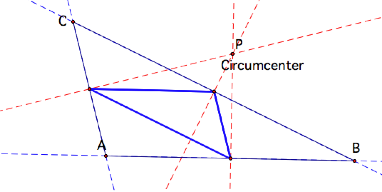
The pedal triangle is still the medial triangle!
Center of Nine Point Circle:
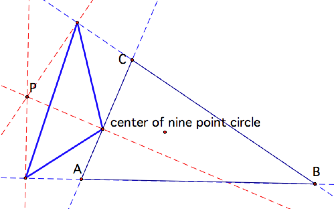
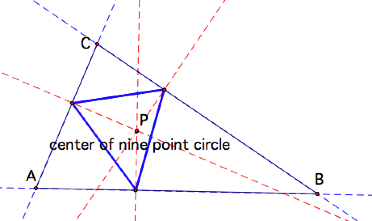
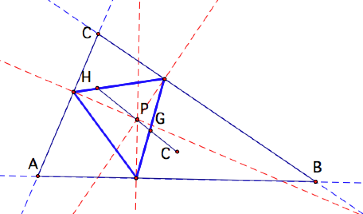
Point P lies on the Euler Line!
More significantly . . . it lies at its midpoint!
Centroid:

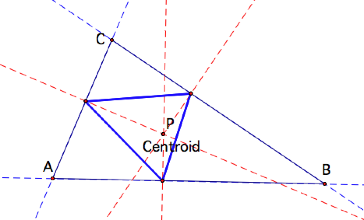
There does not seem to be an obvious relationship when
P is the centroid. Since the other
centers have some type of relationship then there might be something that
exists of which I just have not learned about yet.
Still working on it . . .
What happens when P is
somewhere on the triangle?
If P is one of the vertices
of the triangle:
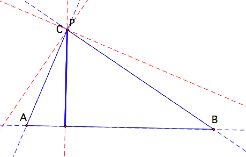
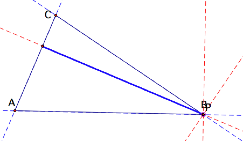
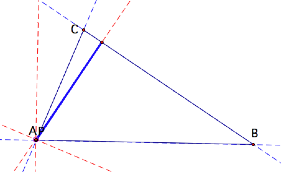
As displayed above when P is one of the vertices then
the the pedal triangle becomes degenerate.
If P is on a side of the
triangle:
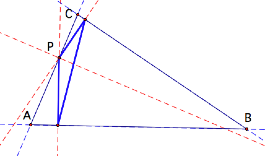
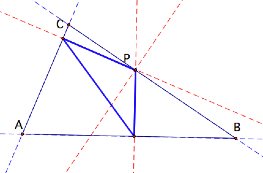
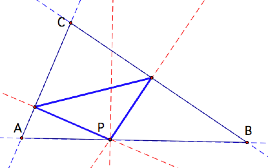
At first glance when P is located on a side of the
triangle nothing extraordinary appears.
However when exploring some angle measures on GSP it seems that
something special does exist as illustrated in the figures below.
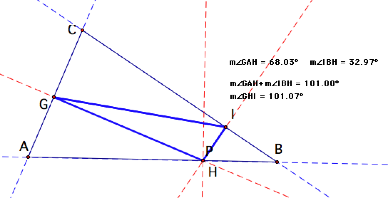
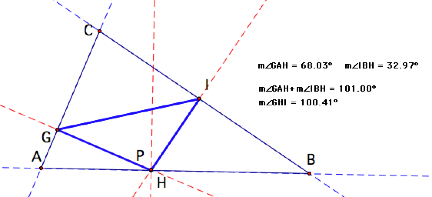
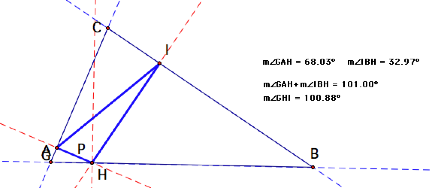
No matter where P is on segment AB, the measure of
angle GHI (or rather angle GPI) is equal to the sum of the two angles that
segment AB is between.
Why is this?
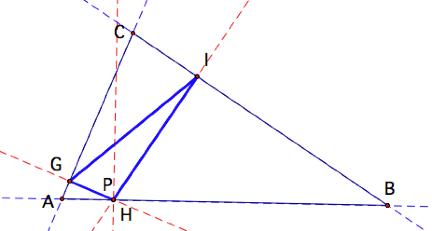
To simplify things
let:
a = measure of angle GAH
b = measure of angle GHA
c = measure of angle IHB
d = measure of angle IBH
e = measure of angle GHI
Want to Prove: a + d = e
Proof:
By construction, the measure
of angle AGH = 90 and the measure of angle BIH = 90.
Since the sum of the angles
of a triangle measure 180 then
a + b + angle AGH = 180 and c
+ d + angle BIH = 180.
Therefore a + b = 90 and c +
d = 90.
By addition we have a + b + c
+ d = 180.
Since the sum of the angles
that form a line measure 180 then b + e + c = 180.
By transitivity we have a + b
+ c + d = b + e + c.
Therefore a + d = e.
Discussion:
Hmmm . . . there is A LOT
going on with P of the pedal triangle and its respective reference
triangle.
There are a couple of ideas
that occurred for which additional investigations may prove interesting such
as:
Why is P the midpoint of
the Euler Line when P is the center of the nine point circle?
Is there a special name
for the triangle created when P is the centroid?